Теорема о кинетической энергии точки в дифференциальной форме
Умножая скалярно обе части уравнения движения материальной точки на элементарное перемещение точки получим
![]()
или, так как , то
![]()
Скалярная величина или половина произведения массы точки на квадрат ее скорости называется кинетической энергией точки или живой силой точки.
Последнее равенство составляет содержание теоремы о кинетической энергии точки в дифференциальной форме, которая гласит: дифференциал кинетической энергии точки равен элеменарной работе, действующей на точку силы.
Физический смысл теоремы о кинетической энергии заключается в том, что работа, производимая действующей на точку силой, накапливается в ней как кинетическая энергия движения.
Теорема о кинетической энергии точки в интегральной форме
Пусть точка переместилась из положения Л в положение В, пройдя по своей траектории конечную дугу АВ (рис. 113). Интегрируя в пределах от Л до Б равенство:
![]()

где соответственно скорости точки в положениях А и В.
Последнее равенство составляет содержание теоремы о кинетической энергии точки в интегральной форме, которая гласит: изменение кинетической энергии точки за некоторый промежуток времени равно работе, совершенной за то же время действующей на нее силой.

Полученная теорема справедлива при движении точки под действием любой силы. Однако, как указывалось, для вычисления полной работы силы нужно в общем случае знать уравнения движения точки.
Поэтому теорема о кинетической энергии, вообще говоря, не дает первого интеграла уравнений движения.
Интеграл энергии
Теорема о кинетической энергии дает первый интеграл урав нений движения точки, если полная работа силы может быть определена, не прибегая к уравнениям движения. Последнее, возможно, как ранее указывалось, если сила, действующая на точку, принадлежит к силовому полю. В этом случае достаточно знать только траекторию точки. Пусть траектория точки будет некоторая кривая, тогда координаты ее точек можно выразить через дугу траектории, и, следовательно, сила зависящая от координат точки, может быть выражена через
и теорема о кинетической энергии дает первый интеграл вида

где - дуги траектории, соответствующие точкам А и - проекция силы на касательную к траектории (рис. 113).
Потенциальная энергия и закон сохранения механической энергии точки
Особый интерес представляет движение точки в потенциальном поле, так как теорема о кинетической энергии дает при этом весьма важный интеграл уравнений движения.
В потенциальном поле полная работа силы равна разности значений силовой функции в конце и в начале пути:
![]()
Следовательно, теорема о кинетической энергии в этом случае записывается в виде:
![]()
Силовая функция, взятая с обратным знаком называется потенциальной энергией точки и обозначается буквой П:
Потенциальная энергия, так же как и силовая функция, задается с точностью до произвольной постоянной, значение которой определяется выбором нулевой поверхности уровня. Сумма кинетической и потенциальной энергии точки называется полной механической энергией точки.
Теорема о кинетической энергии точки, если сила принадлежит к потенциальному полю, записывается в виде:
![]()
где - значения потенциальной энергии, соответствующие точкам А и В. Полученное уравнение составляет содержание закона сохранения механической энергии для точки, который гласит: при движении в потенциальном поле сумма кинетической и потенциальной энергии точки остается постоянной.
Так как закон сохранения механической энергии справедлив только для сил, принадлежащих потенциальным полям, то силы такого поля называются консервативными (от латинского глагола conservare - сохранять), чем подчеркивается выполнение в этом случае сформулированного закона. Заметим, что если понятие кинетической энергии имеет в своем определении известные физические основания, то понятие потенциальной энергии этого лишено. Понятие потенциальной энергии в известном смысле является фиктивной величиной, которая определяется так, что изменения ее значения в точности соответствуют изменениям кинетической энергии. Введение этой величины, связанной с движением, помогает описанию движения и благодаря этому играет существенную роль в так называемом энергетическом описании движения, разрабатываемый аналитической механикой. В последнем и заключается смысл введения этой величины.
Кинетическая энергия.
Неотъемлемым свойством материи является движение. Различные формы движения материи способны к взаимным превращениям, которые, как установлено, происходят в строго определенных количественных соотношениях. Единой мерой различных форм движения и типов взаимодействия материальных объектов и является энергия.
Энергия зависит от параметров состояния системы, ᴛ.ᴇ. таких физических величин, которые характеризуют некоторые существенные свойства системы. Энергию, зависящую от двух векторных параметров, характеризующих механическое состояние системы, а именно, радиус-вектора , определяющего положение одного тела относительно другого, и скорости , определяющей быстроту перемещения тела в пространстве, называют механической.
В классической механике представляется возможным разбить механическую энергию на два слагаемых, каждое из которых зависит только от одного параметра:
где - потенциальная энергия, зависящая от относительного расположения взаимодействующих тел; - кинетическая энергия, зависящая от скорости движения тела в пространстве.
Механическая энергия макроскопических тел может изменяться только за счет работы.
Найдем выражение для кинетической энергии поступательного движения механической системы. Стоит сказать, что для начала рассмотрим материальную точку массой m . Допустим, что ее скорость в некоторый момент времени t равна . Определим работу результирующей силы , действующей на материальную точку в течение некоторого времени:
Учитывая, что на основе определения скалярного произведения
где - начальная, а - конечная скорость точки.
Величина
принято называть кинетической энергией материальной точки.
С помощью этого понятия соотношение (4.12) запишется в виде
Из (4.14) следует, что энергия имеет такую же размерность, как и работа͵ и следовательно, измеряется в тех же единицах.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, работа результирующей всех сил, действующих на материальную точку, равна приращению кинетической энергии этой точки. Отметим, что приращение кинетической энергии может быть положительным или отрицательным в зависимости от знака, совершенной работы (сила может либо ускорять, либо тормозить движение тела). Данное утверждение принято называть теоремой о кинетической энергии.
Полученный результат без труда обобщается на случай поступательного движения произвольной системы материальных точек. Кинетической энергией системы принято называть сумма кинетических энергий материальных точек, из которых эта система состоит. В результате сложения соотношений (4.13) для каждой материальной точки системы, снова получится формула (4.13), но уже для системы материальных точек:
где m – масса всей системы.
Отметим, что имеется существенное отличие теоремы о кинетической энергии (закона об изменении кинетической энергии) и закона об изменении импульса системы. Как известно, приращение импульса системы определяется только внешними силами. Внутренние силы вследствие равенства действия и противодействия не меняют импульс системы. Не так обстоит дело в случае кинетической энергии. Работа внутренних сил, вообще говоря, не обращается в нуль. К примеру, при движении двух материальных точек, взаимодействующих между собой силами притяжения, каждая из сил совершит положительную работу, и будет положительной приращение кинетической энергии всей системы. Следовательно, приращение кинетической энергии определяется работой не только внешних, но и внутренних сил.
Криволинейным интегралом 2-го рода, вычисление которого, как правило, проще, чем вычисление криволинейного интеграла 1-го рода. Мощностью силыf называется работа силы в единицу времени. Так как за бесконечно малое время dt сила совершает работу dA = fsds = fdr, то мощность...
Работа равнодействующей всех сил , приложенных к телу, равна изменению кинетической энергии тела.
Эта теорема верна не только для поступательного движения твердого тела, но и в случае его произвольного движения.
Кинетической энергией обладают только движущиеся тела, поэтому ее называют энергией движения.
§ 8. Консервативные (потенциальные) силы.
Поле консервативных сил
Опр.
Силы, работа которых не зависит от пути, по которому двигалось тело, а определяется только начальным и конечным положениями тела, называются консервативными (потенциальными) силами.
Опр.
Поле сил – область пространства, в каждой точке которого на тело, помещенное туда, действует сила, закономерно меняющаяся от точки к точке пространства.
Опр.
Поле, не изменяющееся со временем, называется стационарным.
Можно доказать следующие 3 утверждения
1) Работа консервативных сил по любому замкнутому пути равна 0.
Доказательство:
2) Однородное поле сил консервативно.
Опр.
Поле называется однородным, если во всех точках поля силы, действующие на тело помещенное туда, одинаковы по модулю и направлению.
Доказательство:
3) Поле центральных сил, в котором величина силы зависит только от расстояния до центра, консервативно.
Опр.
Поле центральных сил – силовое поле, в каждой точке которого на точечное тело, движущееся в нем, действует сила, направленная вдоль линии, проходящей через одну и ту же неподвижную точку – центр поля.
В общем случае такое поле центральных сил не является консервативным. Если же в поле центральных сил величина силы зависит только от расстояния до центра силового поля (О), т.е. , то такое поле является консервативным (потенциальным).
Доказательство:
где - первообразная .
§ 9. Потенциальная энергия.
Связь силы и потенциальной энергии
в поле консервативных сил
Полем консервативных сил выберем начало координат, т.О.
Потенциальная энергия тела в поле консервативных сил. Эта функция определяется однозначно (зависит только от координат), т.к. работа консервативных сил не зависит от вида пути.
Найдем связь в поле консервативных сил при перемещении тела из точки 1 в точку 2.
Работа консервативных сил равна изменению потенциальной энергии с обратным знаком.
Потенциальная энергия тела поля консервативных сил есть энергия, обусловленная наличием силового поля, возникающего в результате определенного взаимодействия данного тела с внешним телом (телами), которое, как говорят, и создает силовое поле.
Потенциальная энергия поля консервативных сил характеризует способность тела совершить работу и численно равна работе консервативных сил по перемещению тела в начало координат (или в точку с нулевой энергией). Она зависит от выбора нулевого уровня и может быть отрицательной. В любом случае , а значит и для элементарной работы справедливо , т.е. или , где - проекция силы на направление движения или элементарное перемещение. Следовательно, . Т.к. мы можем перемещать тело в любом направлении, то для любого направления справедливо . Проекция консервативной силы на произвольное направление равна производной потенциальной энергии по этому направлению с обратным знаком.
Учитывая разложение векторов и по базису , , получим, что
С другой стороны из математического анализа известно, что полный дифференциал функции нескольких переменных равен сумме произведений частных производных по аргументам на дифференциалы аргументов, т.е. , а значит, из соотношения получим
Для более компактной записи данных соотношений можно использовать понятие градиента функции.
Опр.
Градиентом некоторой скалярной функции координат называется вектор с координатами, равными соответствующим частным производным этой функции.
В нашем случае
Опр.
Эквипотенциальной поверхностью называется геометрическое место точек в поле консервативных сил, значения потенциальной энергии в которых одинаковы, т.е. .
Т.к. из определения эквипотенциальной поверхности следует, что для точек этой поверхности, то , как производная константы, следовательно .
Таким образом, консервативная сила всегда перпендикулярна эквипотенциальной поверхности и направлена в строну убыли потенциальной энергии. (П 1 >П 2 >П 3).
§ 10. Потенциальная энергия взаимодействия.
Консервативные механические системы
Рассмотрим систему их двух взаимодействующих частиц. Пусть силы их взаимодействия центральные и величина силы зависит от расстояния между частицами (такими силами являются гравитационные и электрические кулоновские силы). Понятно, что силы взаимодействия двух частиц – внутренние.
Учитывая третий закон Ньютона (), получим , т.е. работа внутренних сил взаимодействия двух частиц определяется изменением расстояния между ними.
Такая же работа была бы совершена, если бы первая частица покоилась в начале координат, а вторая – получила перемещение , равное приращению ее радиус-вектора, т.е работу, совершаемую внутренними силами можно вычислять, считая одну частицу неподвижной, а вторую – движущейся в поле центральных сил, величина которых однозначно определяется расстоянием между частицами. В §8 мы доказали, что поле таких сил (т.е. поле центральных сил, в котором величина силы зависит только от расстояния до центра) консервативно, а значит, их работу можно рассматривать как убыль потенциальной энергии (определяемой, согласно §9, для поля консервативных сил).
В рассматриваемом случае эта энергия обусловлена взаимодействием двух частиц, составляющих замкнутую систему. Ее именуют потенциальной энергией взаимодействия (или взаимной потенциальной энергией). Она также зависит от выбора нулевого уровня и может быть отрицательной.
Опр.
Механическая система твердых тел, внутренние силы между которыми консервативны, называется консервативной механической системой.
Можно показать, что потенциальная энергия взаимодействия консервативной системы из N частиц слагается из потенциальных энергий взаимодействия частиц, взятых попарно, что можно представить.
Где - потенциальная энергия взаимодействия двух частиц i-ой и j-ой. Индексы i и j в сумме принимают независимые друг от друга значения 1,2,3, … , N. Учитывая, что одна и та же потенциальная энергия взаимодействия i-ой и j-ой частиц друг с другом, то при суммировании энергия будет умножаться на 2, вследствие чего появляется коэффициент перед суммой. В общем случае потенциальная энергия взаимодействия системы из N частиц будет зависеть от положения или координат всех частиц . Нетрудно видеть, что потенциальная энергия частицы в поле консервативных сил есть разновидность потенциальной энергии взаимодействия системы частиц, т.к. силовое поле есть результат некоторого взаимодействия тел друг с другом.
§ 11. Закон сохранения энергии в механике.
Пусть твердое тело движется поступательно под действием консервативных и неконсервативных сил, т.е. общий случай. Тогда равнодействующая всех сил, действующих на тело . Работа равнодействующей всех сил в этом случае .
По теореме о кинетической энергии , а также учитывая, что , получим
Полная механическая энергия тела
Если , то . Это и есть математическая запись закона сохранения энергии в механике для отдельного тела.
Формулировка закона сохранения энергии:
Полная механическая энергия тела не изменяется в отсутствии работы неконсервативных сил.
Для механической системы из N частиц нетрудно показать, что (*) имеет место.
При этом
Первая сумма здесь – суммарная кинетическая энергия системы частиц.
Вторая – суммарная потенциальная энергия частиц во внешнем поле консервативных сил
Третья – потенциальная энергия взаимодействия частиц системы друг с другом.
Вторая и третья суммы представляют собой полную потенциальную энергию системы.
Работа неконсервативных сил состоит из двух слагаемых, представляемых собой работу внутренних и внешних неконсервативных сил .
Также как и в случае движения отдельного тела, для механической системы из N тел, если , то , и закон сохранения энергии в общем случае для механической системы гласит:
Полная механическая энергия системы частиц, находящихся только под действием консервативных сил, сохраняется.
Таким образом, при наличии неконсервативных сил полная механическая энергия не сохраняется.
Неконсервативными силами являются, например, сила трения , сила сопротивления и другие силы, действия которых вызывают дессинацию энергии (переход механической энергии в теплоту).
Силы, приводящие к дессинации называются дессинативными. Некоторые силы не обязательно являются дессинативными.
Закон сохранения энергии имеет всеобщий характер и применим не только к механическим явлениям, но и ко всем процессам в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным. Энергия лишь может переходить из одной формы в другую.
С учетом этого равенства
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.
Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.
Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.
Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.
Кинетическая энергия
Рассмотрим случай, когда на тело массой m действует постоянная сила \(~\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(~\vec F\) и перемещения \(~\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F ∙s . Модуль силы по второму закону Ньютона равен F = m∙a , а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ 1 и конечной υ 2 скорости и ускорения а выражением \(~s = \frac{\upsilon^2_2 - \upsilon^2_1}{2a}\) .
Отсюда для работы получаем
\(~A = F \cdot s = m \cdot a \cdot \frac{\upsilon^2_2 - \upsilon^2_1}{2a} = \frac{m \cdot \upsilon^2_2}{2} - \frac{m \cdot \upsilon^2_1}{2}\) . (1)
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела .
Кинетическая энергия обозначается буквой E k .
\(~E_k = \frac{m \cdot \upsilon^2}{2}\) . (2)
Тогда равенство (1) можно записать в таком виде:
\(~A = E_{k2} - E_{k1}\) . (3)
Теорема о кинетической энергии
работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.
Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.
Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ , то работа силы равна конечному значению кинетической энергии тела:
\(~A = E_{k2} - E_{k1}= \frac{m \cdot \upsilon^2}{2} - 0 = \frac{m \cdot \upsilon^2}{2}\) . (4)
Физический смысл кинетической энергии
кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел.
Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Потенциальными называются силы , работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.
При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.
Силы , работа которых зависит от формы траектории, называются непотенциальными . При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.
Потенциальная энергия взаимодействия тела с Землей
Найдем работу, совершаемую силой тяжести F т при перемещении тела массой m вертикально вниз с высоты h 1 над поверхностью Земли до высоты h 2 (рис. 1). Если разность h 1 – h 2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F т во время движения тела можно считать постоянной и равной mg .
Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна
\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)
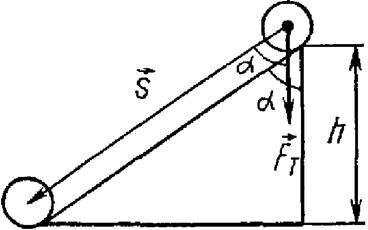
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F т = m∙g совершает работу
\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)
где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.
Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h ’, h ’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:
\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\) , (7)
где h 1 и h 2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С .

Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.
При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.
Равенство (7) можно представить в таком виде:
\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)
Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.
Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h 2 , в точку, расположенную на высоте h 1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.
\(~A = - (E_{p2} - E_{p1})\) . (9)
Потенциальная энергия обозначается буквой Е p .
Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
При таком выборе нулевого уровня потенциальная энергия Е p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:
\(~E_p = m \cdot g \cdot h\) . (10)
Физический смысл потенциальной энергии взаимодействия тела с Землей
потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.
В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m , находящееся на высоте h , где h < h 0 (h 0 – нулевая высота), обладает отрицательной потенциальной энергией:
\(~E_p = -m \cdot g \cdot h\) .
Потенциальная энергия гравитационного взаимодействия
Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М , находящихся на расстоянии r одна от другой, равна
\(~E_p = G \cdot \frac{M \cdot m}{r}\) . (11)
где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е p = 0) принят при r = ∞.
Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M e – масса Земли, R e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.
\(~E_e = G \cdot \frac{M_e \cdot m \cdot h}{R_e \cdot (R_e +h)}\) . (12)
При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R e) равна
\(~E_p = m \cdot g \cdot h\) ,
где \(~g = G \cdot \frac{M_e}{R^2_e}\) – модуль ускорения свободного падения вблизи поверхности Земли.
Потенциальная энергия упруго деформированного тела
Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x 1 до конечного значения x 2 (рис. 4, б, в).

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x ) и умножить на модуль перемещения:
\(~A = F_{upr-cp} \cdot (x_1 - x_2)\) , (13)
где \(~F_{upr-cp} = k \cdot \frac{x_1 - x_2}{2}\) . Отсюда
\(~A = k \cdot \frac{x_1 - x_2}{2} \cdot (x_1 - x_2) = k \cdot \frac{x^2_1 - x^2_2}{2}\) или \(~A = -\left(\frac{k \cdot x^2_2}{2} - \frac{k \cdot x^2_1}{2} \right)\) . (14)
Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
\(~E_p = \frac{k \cdot x^2}{2}\) . (15)
Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:
\(~A = -(E_{p2} - E_{p1})\) . (16)
Если x 2 = 0 и x 1 = х , то, как видно из формул (14) и (15),
\(~E_p = A\) .
Физический смысл потенциальной энергии деформированного тела
потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.
Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано . Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:
\(~A = -(E_{p2} - E_{p1})\) . (17)
По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:
\(~A = E_{k2} - E_{k1}\) . (18)
Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:
\(~E_{k2} - E_{k1} = -(E_{p2} - E_{p1})\) или \(~E_{k1} + E_{p1} = E_{k2} + E_{p2}\) . (19)
Закон сохранения энергии в механических процессах :
сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.
Сумма кинетической и потенциальной энергии тел называется полной механической энергией .
Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е p = m∙g∙h ). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.
В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.
Закон сохранения энергии раскрывает физический смысл понятия работы :
работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.
Закон об изменении механической энергии
Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:
\(~A_{vn} = \Delta E = E - E_0\) . (20)
где Е и Е 0 – полные механические энергии системы в конечном и начальном состояниях соответственно.
Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F r тела составляет π радиан, работа силы трения отрицательна и равна
\(~A_{tr} = -F_{tr} \cdot s_{12}\) ,
где s 12 – путь тела между точками 1 и 2.
Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.
Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
Закон сохранения и превращения энергии
при любых физических взаимодействиях энергия превращается из одной формы в другую.
Иногда угол между силой трения F tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:
\(~A_{tr} = F_{tr} \cdot s_{12}\) ,
Пример 1 . Пусть, внешняя сила F действует на брусок В , который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F tr2 , действующей на тележку со стороны бруска, положительна:

Пример 2 . При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Литература
- Кабардин О.Ф. Физика: Справ. материалы: Учеб. пособие для учащихся. – М.: Просвещение, 1991. – 367 с.
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
- Элементарный учебник физики: Учеб. пособие. В 3 т. / Под ред. Г.С. Ландсберга: т. 1. Механика. Теплота. Молекулярная физика. – М.: Физматлит, 2004. – 608 с.
- Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступающих в вузы и самообразования. – М.: Наука, 1983. – 383 с.
